Photonic crystals, also known as photonic band gap materials, are the subject of numerous investigations because of their unique characteristics, with prospective applications ranging from gas sensing to optical filters, inkless printing, and reflective displays. Photonic crystals are highly ordered materials with a periodic dielectric constant, whose period is on the order of the wavelength (or wavelength range) of interest. The effect of confining and controlling light propagation stems from the photonic band gap, a band of frequencies in which light propagation in the photonic crystal is forbidden. It is possible to design 1D, 2D, and 3D photonic crystals through variations in the refractive index and periodicity.
To combat the issues with using flat emitters, researchers turn their attention to 3D microLEDs. Such emitters have the obvious advantage of increased surface area. Further, the increased dimensionality allows for the formation of quantum wells on the sides of the emitter. The increased dimensionality also provides access to various crystal faces. In the case of GaN, it includes the m-plane that benefits from a reduced native electric field near the surface, reducing the influence of the quantum confined stark effect (QCSE), thereby increasing emitter efficiency.
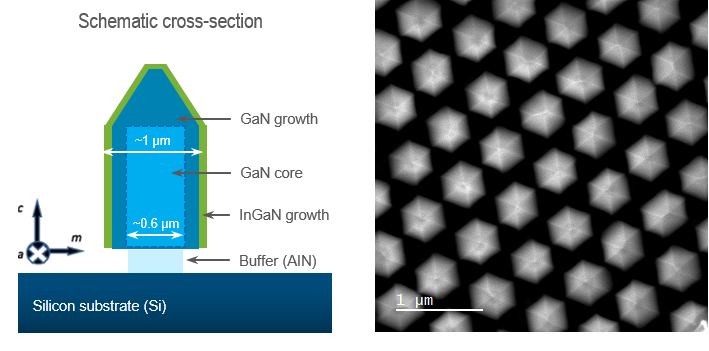
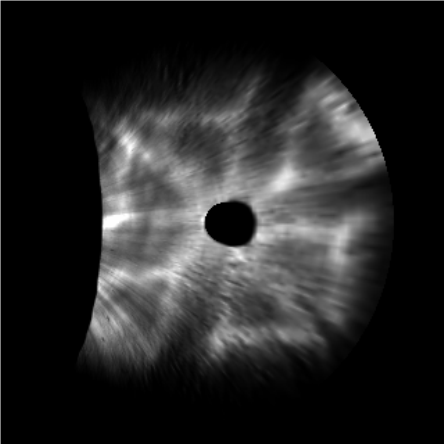
To determine the photonic behavior of such an array, we employ the wavelength and angle-resolved CL (WARCL) technique. The WARCL pattern shows distinct anisotropy at several wavelengths relevant to the pillar material, dimensions, and periodicity.
This shows the anisotropy in the light emission as a function of wavelength, which is directly valuable for potential display technology. However, the wavelength-angle bases are not ideal for analyzing photonic modes; for this, they may transform from wavelength-angle to energy-momentum bases.

In this way, CL is useful for probing the local density of optical states (LDOS) in the photonic specimen, which is paramount in designing nanophotonic structures.
 |
Determining photonic band structure by energy-momentum spectroscopy in an electron microscope |